Posted Updated Algorithms17 minutes read (About 2521 words)

Algorithm: leetcode

导言

计算机笔试，以及华为可信科目一相关的常见算法。

渐进符号

排序算法

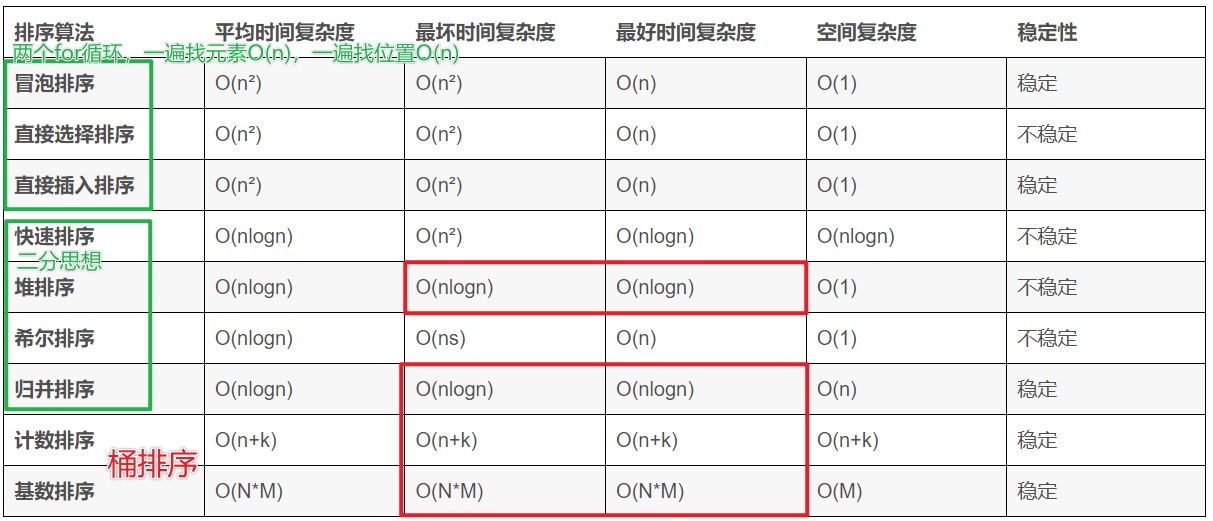
  • 排序算法的稳定性：排序前后相同元素的相对位置不变，则称排序算法是稳定的；否则排序算法是不稳定的。
  • 计数排序 中 k是数据出现的范围
  • 基数排序时间复杂度为O(N*M)，其中N为数据个数，M为数据位数。

按照实现方法分类

  • 选择排序

    • 直接选择排序：N轮，每轮变小的范围内找到最小值，然后与第i个交换。
    • 堆排序：
      • 最大堆与数组的映射关系 大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
      • 维护每轮范围变小的堆，每次将最大的堆顶移动到最后。每次维护堆需要O(logn)交换，把pop上来的小元素沉底到叶节点。
      • 初始建堆需要O(nlogn)

  • 插入排序

    • 直接插入：N轮，每轮从i开始向前插入（移动来交换），直到插入到合适的位置
    • 希尔排序: 希尔排序是插入排序改良的算法，
      • 希尔排序步长从大到小调整，第一次循环后面元素逐个和前面元素按间隔步长进行比较并交换，
      • 直至步长为1，步长选择是关键。

  • 交换排序

    • 冒泡排序：冒泡N轮，每轮变小的范围内确定最后一个。
    • 快速排序：在数组中随机选一个数（默认数组首个/末尾元素），数组中小于等于此数的放在左边部分(交换到前面的排列)，大于此数的放在右边部分，这个操作确保了这个数是处于正确位置的，再对左边部分数组和右边部分数组递归调用快速排序，重复这个过程。

  • 分治合并

    • 归并排序： 首先让数组中的每一个数单独成为长度为1的区间，然后两两一组有序合并，得到长度为2的有序区间，依次合并进行得到长度为4、8、16的区间，直到合成整个区间。

  • 计数排序：数据出现的范围k << O(n)时，或者k=O(n)都可以采用该方法。

  • 基数排序：对数据的每一位(共M位)从低位到高位进行stableSort。大部分时候选择计数排序O(N+k)。总时间复杂度O(M*(N+k))

  • 桶排序：类似计数排序的思想，但是一般是对于区间等分为桶。桶内可以采用插入排序。n个元素n个桶，数学期望是O(n)

堆排序代码细节

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
void heapSort(int array[], int n)
{
    int i;
    //先建立堆
    for (i=n/2;i>0;i--)
    {
        HeapAdjust(array,i,n);//从下向上，从右向左调整
    }
    //交换最大堆顶，重复n次
    for( i=n;i>1;i--)
    {
        swap(array, 1, i);
        HeapAdjust(array, 1, i-1);//从上到下，从左向右调整
    }
}
void HeapAdjust(int array[], int s, int n )
{
    int i,temp;
    temp = array[s];
    for(i=2*s;i<=n;i*=2)
    {
        if(i<n&&array[i]<array[i+1])
        {
            //交换左右子树最大的那个
            i++;
        }
        if(temp>=array[i])
        {
            //找到了插入的合适的位置，子节点更小，父节点更大
            break;
        }
        // 将节点向上移动
        array[s]=array[i];
        s=i;
    }
    //将最顶部插入到合适的位置
    array[s]=temp;
}
void swap(int array[], int i, int j)
{
    int temp;
    temp=array[i];
    array[i]=array[j];
    array[j]=temp;
}

排序相关的问题

  • 既然时间复杂度堆排序、归并排序好于快排，为什么C++的qsort使用的是快排
    • 快速排序访存更友好，堆排序访问是跳跃的
    • 对于同样的数据，排序过程中，堆排序算法的数据交换次数多于快排
      • 堆排序建立堆，与堆顶的交换，很多时候都是无用功
    • 在数据量小的时候快速排序当属第一，堆排序最差，但随着数据的不断增大归并排序的性能会逐步赶上并超过快速排序，性能成为三种算法之首。
  • C++ 的 stable_sort 是基于归并排序的

LeetCode 常见算法

拓扑排序

拓扑排序常用来确定一个依赖关系集(图关系)中，事物发生的顺序。

带信号量判断的无依赖队列来实现，入队无依赖集合，出队的无依赖元素(add to result)去除后续元素的依赖信号量，信号量为0代表无依赖，可以入队。

无环图（树图）中最长距离

找到图中距离最远的两个节点与它们之间的路径：

  • 以任意节点 p 出现，利用广度优先搜索或者深度优先搜索找到以 p 为起点的最长路径的终点 x；
  • 以节点 x 出发，找到以 x 为起点的最长路径的终点 y；
  • x 到 y 之间的路径即为图中的最长路径，找到路径的中间节点即为根节点。

证明

  • p->x 一定是最长路径的一部分
  • x->y 是x为起点的最长路径，也就是树的最长路径。

树状数组

https://leetcode-cn.com/circle/article/9ixykn/

https://leetcode-cn.com/problems/range-sum-query-mutable/

BFS计算各点距离初始点的最近距离

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//input [[0,1],[1,2]]
//维护
vector<vector<int>> adj(n); //先找出每个点的有关边
vector<bool> visit(n, false);   //维护已访问元素

queue<int> qu;

qu.emplace(0);
visit[0] = true;
int dist = 1;

while (!qu.empty()) {
    int sz = qu.size();
    for (int i = 0; i < sz; ++i) {
        int curr = qu.front();
        qu.pop();
        for (auto & v : adj[curr]) {
            if (visit[v]) {
                continue;
            }
            qu.emplace(v);
            //对应处理
            visit[v] = true;
        }
    }
    dist++;
}

2进制数表示子集合

对集合大小为n，可以用大于等于0小于1<<n的2^n-1个数字来表示子集。

但是对每个子集都会单独计算，有重复。 不如用按每位是否存在回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#2044
class Solution {
public:
    int ans = 0;
    int countMaxOrSubsets(vector<int>& nums) {
        int maxOr = 0;
        for (auto n: nums){
            maxOr = n | maxOr;
        }
        dfs(nums, maxOr, 0 , 0);
        return ans;
    }
    void dfs(vector<int>& nums, int maxOr, int idx, int cur){
        if (cur == maxOr){
            ans += 1 << (nums.size()-idx);
            return;
        }

        if (idx == nums.size()){
            return;
        }

        dfs(nums, maxOr, idx+1, cur | nums[idx]);
        dfs(nums, maxOr, idx+1, cur);

    }
};

2进制表示使用状态true false

int 可以表示32个元素的使用情况

https://leetcode.cn/problems/can-i-win/

前缀和和差分

前缀和
和差分
是一组互逆的方法；他们的关系和积分
与求导
实质是一样的。前缀和可以帮我们通过预处理快速的求出区间的和；差分则可以快速帮助我们记录区间的修改。

将区间前一个加一，最后一个减一实现。

leetcode 798

预处理查询的数组

通过预处理记录信息来减少查询的时间

leetcode 2055

二分法

二分寻找满足条件的最小整数, 注意left + 1 < right和s >= cars

1
2
3
4
5
6
7
8
9
10
11

while (left + 1 < right) { // 开区间
    long long mid = (left + right) / 2, s = 0;
    for (int r : ranks)
        s += sqrt(mid / r);
    (s >= cars ? right : left) = mid;
}
// 作者：灵茶山艾府
// 链接：https://leetcode.cn/problems/minimum-time-to-repair-cars/solutions/2177199/er-fen-da-an-pythonjavacgo-by-endlessche-keqf/
// 来源：力扣（LeetCode）
// 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

直接模拟

最常用的方法

哈希算法

根据设定的哈希函数H（key）和处理冲突方法将一组关键字映象到一个有限的地址区间上的算法。也称为散列算法、杂凑算法。

哈希冲突

一般有：开放定址法、链地址法（拉链法）、再哈希法、建立公共溢出区

LeetCode 代码优化加速

cin.tie与sync_with_stdio加速输入输出

std::ios::sync_with_stdio(); 是一个“是否兼容stdio”的开关，C++为了兼容C，保证程序在使用了std::printf和std::cout的时候不发生混乱，将输出流绑到了一起。也就是 C++标准streams(cin,cout,cerr…) 与相应的C标准程序库文件(stdin,stdout,stderr)同步，使用相同的 stream 缓冲区。
默认是同步的，但由于同步会带来某些不必要的负担，因此该函数作用是使得用户可以自行取消同步。

cin.tie(NULL) 取消 cin 和 cout 的绑定。

这对于输入数据个数在10^5以上的程序十分有效。

1
2
3
4
5
6
7
8
9
10
11
static int x = []() {
    std::ios::sync_with_stdio(false);
    cin.tie(NULL);
    return 0;
}();
// or
static const auto io_sync_off = []() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    return nullptr;
}();

or

1
2
3
4
5
int init = []() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    return 0;
}();

问题拆分循环调用

不如从底层动态规划合并，不要嵌套函数调用，还可以用二维数据，数据局部性较好。

https://leetcode-cn.com/problems/optimal-division/submissions/

不一定要执着数据只遍历一遍

可以将复杂的一次遍历，拆开成两次遍历，一次处理数据并存储，一次遍历统计。速度反而会快

简单递归循环

用while代替函数递归调用，eg二分法

减少if语句

可以保存分支的值来实现(1748)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//0ms
int sumOfUnique(vector<int>& nums) {
 int state[101]{}, ans = 0, d[101]{1,-1};
 for(int x: nums) ans += d[state[x]++] * x;
 return ans;
}

//4ms
int sumOfUnique(vector<int>& nums) {
 array<char,101> isshowed {};
 int sum=0;
 for(auto& num:nums){
  if(isshowed[num]==0){
   isshowed[num]=1;
   sum+=num;
  }else if(isshowed[num]==1){
   isshowed[num]=2;
   sum-=num;
  }
 }
 return sum;
}

通过判断筛选掉

无用的遍历计算(1219)

减少for循环

循环展开，只有一两种情况就不要写for循环了

注意的细节

计算防止溢出

1
int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2

转化成加减，而不用乘法

1
2
3
A < B/2
变成
A < B-A

参考文献

https://oi-wiki.org/dp/basic/

https://github.com/azl397985856/leetcode/blob/master/thinkings/dynamic-programming.md

作者：AC_OIer
链接：https://leetcode-cn.com/problems/the-number-of-good-subsets/solution/gong-shui-san-xie-zhuang-ya-dp-yun-yong-gz4w5/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

Algorithm: leetcode

http://icarus.shaojiemike.top/2023/06/03/Work/Algorithms/algorithm/

Author

Shaojie Tan

Posted on

2023-06-03

Updated on

2025-01-30

Licensed under

#

Like this article? Support the author with

Follow

Categories

Subscribe for updates

follow.it

Links

Recents

Archives

Tags

5G1
64bits vs 32bits1
AI3
AMAT1
AMD3
ASPLOS1
ATI1
AVX2
Algorithm1
Alpha1
Analysis1
Apt1
Assembly4
BFS1
BHive1
BT3
BTL1
Baka Mitai1
Bash1
Big-Endian1
×