RL Algorithms: PPO & GRPO-like
PPO (2017)
PPO(Proximal Policy Optimization)是当前强化学习(RL)中主流的 on-policy 算法之一,因其实现简单、样本效率适中、训练稳定而被广泛应用(如在多模态 RL 或 LLM 的对齐训练中)。
下面逐步解释:
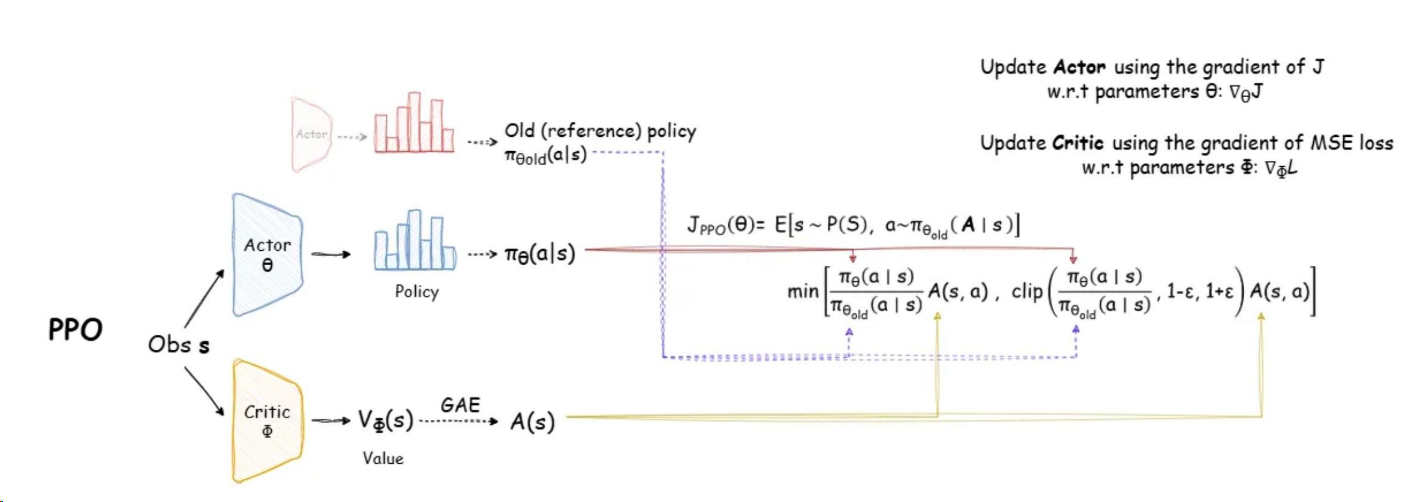
一、PPO 的核心思想
PPO 是一种 策略梯度(Policy Gradient) 方法,目标是直接优化策略 $\pi_\theta(a|s)$,使得期望回报最大化:
$$
\max_\theta \mathbb{E}_{\tau \sim \pi_\theta} \left[ \sum_t \gamma^t r_t \right]
$$
但直接优化容易导致策略更新过大,造成训练崩溃。PPO 通过引入 “信赖域”约束(trust region) 来限制策略更新幅度,从而保证稳定性。
具体做法是使用 重要性采样比例(Importance Sampling Ratio):
$$
r_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{\text{old}}}(a_t|s_t)}
$$
然后构造 Clipped Surrogate Objective:
$$
L^{\text{PPO}}(\theta) = \mathbb{E}_t \left[ \min\left( r_t(\theta) \hat{A}_t,\ \text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon) \hat{A}_t \right) \right]
$$
其中:
- (\hat{A}_t) 是 优势函数(Advantage) 的估计(关键!)
- (\epsilon) 是一个小常数(如 0.2),控制策略更新幅度
二、核心GAE(Generalized Advantage Estimation)
1. 优势函数 (A(s,a)) 的作用
策略梯度中,我们希望知道:
“在状态 (s) 下采取动作 (a),比平均策略好多少?”
这由 优势函数 定义:
$$
A^\pi(s,a) = Q^\pi(s,a) - V^\pi(s)
$$
- (Q^\pi(s,a)):执行动作 (a) 后按策略 (\pi) 继续的回报
- (V^\pi(s)):在状态 (s) 下按策略 (\pi) 继续的期望回报
优势函数 降低方差(相比直接用回报 (R_t)),使训练更稳定。
2. GAE 是优势函数的高效低方差估计器
真实 (A(s,a)) 无法直接计算,GAE 提供一种 偏差-方差权衡 的估计:
$$
\hat{A}t^{\text{GAE}(\gamma,\lambda)} = \sum{l=0}^{T-t-1} (\gamma \lambda)^l \delta_{t+l}
$$
其中:
$$
\delta_t = r_t + \gamma V(s_{t+1}) - V(s_t)
$$
- (\gamma):折扣因子
- (\lambda):GAE 超参((\lambda=0) → 高偏差低方差;(\lambda=1) → 低偏差高方差)
✅ GAE 的优势:
- 利用 learned value function (V(s)) 来减少回报估计的方差
- 通过 (\lambda) 平滑地插值 between Monte Carlo(无偏)和 TD(0)(低方差)
- 是 PPO 稳定训练的关键组件
所以,GAE 不是 PPO 的“可选”组件,而是其高效梯度估计的核心。
三、涉及模型
“为什么需要 reward、reference、value 三个 model”?
这里可能存在一些术语混淆。标准 PPO 并不需要三个独立模型,但某些扩展场景(尤其是 LLM 的强化学习对齐,如 RLHF)会引入额外组件。
我们分情况说明:
✅ 标准 PPO(如 Atari、MuJoCo):
只需要 两个网络(通常共享底层):
- Policy Network(Actor):输出动作分布 (\pi_\theta(a|s))
- Value Network(Critic):输出状态价值 (V_\phi(s)),用于计算 GAE
所以是 两个 head,一个或两个 model,但没有 reward model 或 reference model
✅ 在 LLM + RLHF 场景中(如 InstructGPT、Llama-2-Chat):
为对齐人类偏好,PPO 被用于微调语言模型,此时引入 三个模型:
| 模型 | 作用 | 是否更新 |
|---|---|---|
| Policy Model(Actor) | 当前要优化的 LLM(如 Llama) | ✅ 是,通过 PPO 更新 |
| Reward Model(RM) | 输入 prompt + response,输出人类偏好打分(标量) | ❌ 冻结,不更新 |
| Reference Model | 初始 SFT 模型(监督微调后的 checkpoint) | ❌ 冻结,用于 KL penalty |
此时 reward 并非环境反馈,而是由 Reward Model 预测;同时为防止策略偏离太远,加入 KL 散度惩罚项:
$$
L^{\text{KL}} = \beta \cdot D_{\text{KL}}(\pi_\theta(\cdot|s) | \pi_{\text{ref}}(\cdot|s))
$$
所以,“三个模型”是 RLHF 框架的特征,而非 PPO 本身的必需。
📌 总结:
- 经典 PPO:1 个策略 + 1 个价值网络(共两个模型/heads)
- PPO in LLM(RLHF):Policy + Reward Model + Reference Model(三个)
- Reward Model:提供 reward 信号
- Reference Model:防止策略坍塌或胡说(通过 KL 约束)
- Value Model:依然需要(用于 GAE)
总结
| 问题 | 回答 |
|---|---|
| PPO 核心是什么? | 通过 clipping 机制限制策略更新幅度,保证稳定训练 |
| 为什么 GAE 是核心? | GAE 提供低方差、可调偏差的优势估计,是策略梯度有效的关键 |
| 为什么需要三个模型? | 标准 PPO 不需要;但在 LLM 的 RLHF 场景中,为实现人类偏好对齐,引入了冻结的 Reward Model 和 Reference Model |
如果你是在多模态强化学习或 LLM RL 场景下使用 PPO(如基于 VeRL 框架),那么三个模型的架构确实常见,但其动机来自于 对齐目标 和 稳定性约束,而非 PPO 算法本身。
PPO 初始权重
我们来逐个分析这四个模型在 PPO for LLM(RLHF) 场景中的来源与初始化关系:
✅ 四个模型的角色回顾
| 模型 | 作用 | 是否训练 | 典型来源 |
|---|---|---|---|
| Policy Model | 当前待优化的策略(生成 response) | ✅ 是 | SFT checkpoint |
| Value Model | 估计状态价值 (V(s)),用于 GAE | ✅ 是(通常从头训或微调) | 可能来自 Policy 的副本,但 head 不同 |
| Reward Model (RM) | 给出 prompt + response 的标量 reward | ❌ 否(冻结) | 独立训练的偏好模型(pairwise ranking) |
| Reference Model | 提供 KL 散度基准,防策略崩溃 | ❌ 否(冻结) | 与 Policy 初始相同(即 SFT checkpoint) |
🔑 关键问题:初始权重是否一样?
1. Policy Model 与 Reference Model
✅ 初始完全相同。
两者都初始化自 监督微调(SFT)后的 checkpoint。
在 PPO 开始后:
Policy 被更新;
Reference 冻结,用于计算 KL penalty:
$$
\mathcal{L}^{\text{KL}} = \beta \cdot D_{\text{KL}}\left( \pi_{\theta}(a|s) ,|, \pi_{\text{ref}}(a|s) \right)
$$
这是防止语言模型“过度优化 reward 而胡说八道”的关键机制。
2. Value Model 的初始化
- 通常初始化自 Policy Model 的主干(backbone),但:
- 最后的 LM head 被替换为 scalar value head(一个线性层输出标量);
- 有些实现中,value head 是随机初始化的,主干权重 copy 自 SFT model;
- 也有做法是从头训练 value model(但效率低,不稳定)。
- 所以:主干权重 ≈ Policy 初始权重(即 SFT checkpoint),但输出 head 不同。
📌 示例(如 HuggingFace TRL 或 OpenAI 的 InstructGPT):
2
3
4
reference = AutoModelForCausalLM.from_pretrained("sft_model") # same weights
value = AutoModelForCausalLM.from_pretrained("sft_model")
value.lm_head = nn.Linear(hidden_size, 1) # replace LM head with value headRM 则完全独立:
rm = RewardModel.from_pretrained("rm_model")
3. Reward Model (RM)
- ❌ 权重与其他三个无关。
- RM 是通过 人类偏好数据(如 chosen/rejected pairs) 单独训练的(通常用 ranking loss,如 Bradley-Terry);
- 结构上可能和 LLM 主干相同(如 Llama backbone + reward head),但:
- 训练目标不同
- 数据不同
- 通常不共享任何训练过程
- 因此,RM 的权重 ≠ SFT checkpoint
🧩 总结:初始权重关系图
1 | SFT Checkpoint |
所以:
✅ Policy 与 Reference 初始权重完全相同(都来自 SFT)
✅ Value Model 主干通常 copy 自 SFT(即与 Policy 初始一致),但 head 不同
❌ Reward Model 是独立训练的,权重与其他三个无关
💡 工程提示(结合你的背景)
你在使用 VeRL 或自研框架 做多模态 RL + LLM 对齐时,需要注意:
- 显存优化:Policy 和 Reference 可共享 embedding 等只读参数(若框架支持 weight tying / shared read-only views);
- Value head 初始化:建议用 small init(如 zero-mean Gaussian),避免 GAE 初期偏差过大;
- Reward Model 一致性:确保 RM 的 tokenizer、prompt format 与 Policy 严格一致,否则 reward 会失真;
- NPU 优化:Policy/Reference/Value 主干结构相同,可复用同一份编译图(如 on NPU),仅 head 分支不同,有利于融合算子(如 GMM)优化。
VeRL参数对应 (PPO)
你提出的问题非常精准:如何将 VeRL 的 PPO 配置参数(如 actor_rollout_ref.actor、actor_rollout_ref.rollout、critic.model)与 LLM+RLHF 中“Policy / Reference / Reward / Value” 四个模型的概念对应起来?
我们来系统地拆解 VeRL 框架中这些模块的实际角色,并和理论中的四个模型一一映射。
🔍 一、先明确:VeRL 的模块命名逻辑
VeRL(Vectorized Efficient Reinforcement Learning)是一个面向大模型 PPO 训练的高性能 RL 框架,其设计融合了 actor-critic 架构 和 分布式推理/训练优化。它的配置层级如下:
1 | actor_rollout_ref: |
注意:**actor_rollout_ref 是一个复合组件,包含 actor(Policy)、rollout(推理引擎)** 和 reference(Reference Model) 三者。
🧩 二、理论四模型 ↔ VeRL 实际组件映射
| 理论中的模型(RLHF) | VeRL 中的对应项 | 是否训练 | 权重来源 |
|---|---|---|---|
| Policy Model | actor_rollout_ref.actor |
✅ 是 | Qwen/Qwen3-8B(SFT checkpoint) |
| Reference Model | 隐式包含在 actor_rollout_ref 中(通常和 actor 初始相同但冻结) |
❌ 否 | 同 actor 初始权重(SFT) |
| Value Model (Critic) | critic.model |
✅ 是 | Qwen/Qwen3-8B(主干 copy 自 SFT,但 head 替换为 value head) |
| Reward Model (RM) | 未在该命令中显式配置(通常在 reward pipeline 中加载) | ❌ 否 | 独立训练的 RM(如 Qwen3-RM) |
✅ 关键结论:
actor_rollout_ref.actor= Policyactor_rollout_ref.rollout≠ 模型,而是 用 vLLM 引擎执行 actor(或 ref)前向推理 的工具(用于高效生成 response + logprob)critic.model= Value Network- Reference Model 是
actor_rollout_ref内部另一个冻结的副本(和 actor 初始同源)- Reward Model 通常在
data模块或自定义 reward function 中加载(该脚本省略了,但实际运行时会用到)
消失的Reward Model
- 在 VeRL 中,Reward Model 通常通过 自定义 reward function 注入
- 可能配置在 YAML 或代码中,例如:
1
2def compute_rewards(prompts, responses):
return reward_model(prompts, responses) - 因此,命令行中不直接出现 RM 路径是正常的
但经常实际上并不在使用 Reward Model(RM),而是采用了一种 基于规则或自动评分的 reward 函数(比如格式分 + 答案相似度),常见于数学推理、选择题、判断题等结构化任务(如 MATH、GSM8K 等)。
这意味着PPO 设置不属于典型的 RLHF(Reinforcement Learning from Human Feedback),而更接近 “Supervised Reward + PPO” 或 “Automated Reward Shaping” 的范式。
✅ 修正后的模型角色映射(真实场景)
只有三个模型参与训练和推理:
| 模型 | VeRL 中的对应项 | 是否训练 | 作用 |
|---|---|---|---|
| Policy (Actor) | actor_rollout_ref.actor |
✅ 是 | 生成 response(如数学解答) |
| Reference Model | 隐含在 actor_rollout_ref 中(但当前未启用) |
❌ 否(若 use_kl_loss=False) |
用于 KL penalty(防止策略偏离太远) |
| Value Network (Critic) | critic.model |
✅ 是 | 估计状态价值,用于 GAE |
🚫 Reward Model:不存在
✅ Reward:由规则函数计算(如:reward = 0.5 * format_score + 0.5 * answer_correctness)
🔍 为什么这种设计是合理的?
在 数学推理、编程、选择题等任务中:
- 答案具有客观标准(对/错、匹配/不匹配);
- 人工标注偏好数据(如 RM 所需的 chosen/rejected pairs)成本高;
- 自动评分规则(如正则匹配、AST 比较、字符串相似度)足够可靠。
因此,直接用程序化 reward 替代 RM 是工业界和学术界的常见做法(例如:AlphaCode、LeanDojo、MAmmoTH 等工作)。
GRPO (DeepSeek 2024)
Group Relative Policy Optimization (GRPO)[^11]相对于PPO省略了value model,而是从组中估计baseline,显著减少了资源消耗。
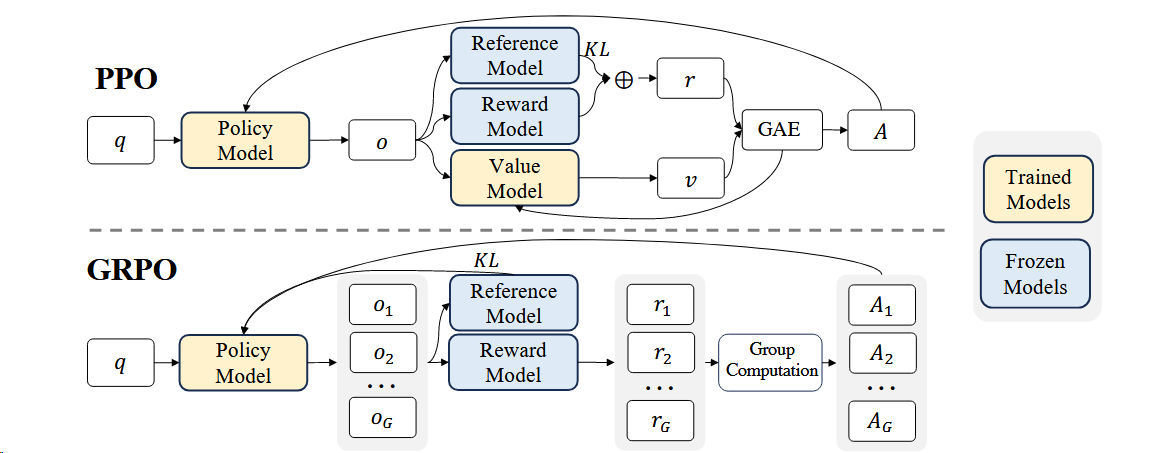
具体来说, 在PPO中,GAE需要与policy model一起训练value model,来减轻奖励模型的过度优化,标准方法是在每个token的reward中添加来自reference模型的每个token的KL惩罚
1. 用多回答均值替代 GAE(优势估计)
PPO:依赖 critic(value network)估计状态价值 (V(s)),再通过 GAE 计算优势 (\hat{A}_t)。
GRPO:不要 critic!对同一个 prompt 生成 (K) 个 responses(即
rollout_n=K),用这 (K) 个 reward 的样本均值作为 baseline,计算每个 response 的中心化 reward:$$
\tilde{r}^{(i)} = r^{(i)} - \frac{1}{K} \sum_{j=1}^K r^{(j)}
$$这个 $\tilde{r}^{(i)}$ 直接替代了 PPO 中的 $\hat{A}_t$。
✅ 这本质上是一种 无 critic 的优势估计,假设同一 prompt 下不同 response 的 reward 波动反映了“好坏相对性”。
2. KL 散度定义一样在 policy 与 reference 之间(而非 policy 与旧 policy)
标准 PPO:KL penalty 通常用于 LLM RLHF 中约束新策略 $\pi_\theta$ 与 **reference model $\pi_{\text{ref}}$**(SFT checkpoint)的距离。
GRPO:明确将 KL 项写为:
$$
\mathcal{L}^{\text{KL}} = \beta \cdot D_{\text{KL}}\left( \pi_{\theta}(\cdot|s) ,|, \pi_{\text{ref}}(\cdot|s) \right)
$$而不是像某些 PPO 实现那样用 old policy($\pi_{\text{old}}$)做 KL。
✅ 这和你观察到的 VeRL 中
compute_old_logp(用于 importance ratio)和compute_ref_logp(用于 KL)的分离是一致的。
3. 完全移除了 Value Network(Critic)
- GRPO 不需要训练 critic,省去了:
- critic 模型的显存
- critic 的训练超参(lr、batch size 等)
- GAE 的 (\lambda, \gamma) 调参
- 这极大简化了系统,尤其适合 reward 可靠、任务结构清晰 的场景(如你的数学题)。
4. Policy Update 使用 “平均梯度” 而非 clipped ratio
GRPO 的 loss 为:
$$
\mathcal{L}^{\text{GRPO}} = -\mathbb{E}{i=1}^K \left[ \tilde{r}^{(i)} \cdot \log \pi_\theta(a^{(i)}|s) \right] + \beta \cdot D{\text{KL}}(\pi_\theta | \pi_{\text{ref}})
$$没有 importance sampling ratio,也没有 clipping!
相当于把每个 response 看作一个样本,用 中心化 reward 作为权重,直接做加权 MLE。
💡 这比 PPO 更简单,但依赖 多回答采样(rollout_n > 1) 来获得 reward 方差估计。
5. 对并行采样的强依赖
- GRPO 要求 每次训练 step 对每个 prompt 生成 K 个 response(通常 K=4~16)。
- 这对 rollout 引擎(如 vLLM)的 batched generation 能力要求高。
- VeRL 正好通过
rollout_n控制这个行为,天然适配 GRPO。
6. 更适合“轨迹级 reward”任务
- GRPO 假设 整个 response 对应一个 scalar reward(如 0/1 正确性),而不是 step-wise reward。
- 这和 LLM 生成任务天然匹配(端到端 reward),而 PPO 最初为 step-wise RL(如 Atari)设计。
- GRPO 本质是 PPO 在 LLM + 自动 reward 场景下的简化特化版:
- 去掉 critic → 降低系统复杂度
- 用多回答采样替代 GAE → 避免 critic 训练不稳定
- 保留 KL(ref) → 防止语言退化
DAPO (2503 字节&清华)
GRPO的问题:
- RL流程细节不够,难复现,复现效果差: GRPO 基线存在几个关键问题,如熵崩塌、奖励噪声和训练不稳定性。
- KL 散度非必须:作者认为long-CoT reasoning model不需要和原本模型保持相似。
- 奖励模型非必要:作者使用了基于规则的奖励建模(通过规则计算奖励)
提出Decouple Clip and Dynamic sAmpling Policy Optimization,DAPO[^12]
为了修复GRPO的策略退化问题提出了一下的trick:
- 裁剪偏移(Clip-Shifting)
- 问题:熵坍缩
- 方法:提高了clip高裁切的参数值,来允许低概率token快速提升概率。
- 动态采样(Dynamic Sampling)
- 问题:推理(采样)出来分数全为 0,或者1的case,是没有优势,对训练是无效的
- 方法:剔除这些case,一直推理直到batch填满。
- Token级策略梯度损失(Token-Level Policy Gradient Loss),在长思维链 RL 场景中至关重要;
- 问题:基于sample的loss计算,会导致CoT里长文本回答不被重视,从而导致长文本质量差,相应长度不正常的变化(不是缓慢增长)
- 方法:使用基于token的loss计算。
- 溢出奖励塑造(Overflowing Reward Shaping),减少奖励噪声并稳定训练。
- 问题: GRPO 原本对于超出response长度的回答都一刀切的惩罚,这会导致模型confused。
- 方法:
1. Overlong Filtering strategy:屏蔽截断样本的损失。
2. Soft Overlong Punishment: 引入临界长度缓冲区,来对超长序列给予与长度正相关的连续的惩罚值。
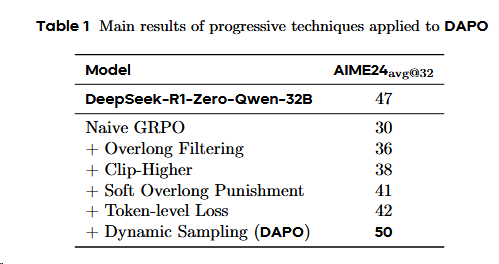
但同时字节DAPO的工作受到质疑:
- 过于工程(trick)、不够优雅、trick是否合理受到争议、
- 训练时间似乎也相对GRPO翻倍。动态采样增加20%的生成开销
- Overfitting的风险:文章提到在训练集上reward很高,但在验证集上效果不明显,这意味着存在过拟合的风险。
🔍 一、“Entropy Collapse” 是什么?
1. 策略熵(Policy Entropy)的定义
在强化学习中,策略 (\pi(a|s)) 是一个概率分布(对 LLM 来说,是 token 的 softmax 分布)。其熵定义为:
$$
H[\pi(\cdot|s)] = -\sum_a \pi(a|s) \log \pi(a|s)
$$
- 高熵:策略输出多样,不确定性强(如 softmax 接近 uniform)→ 探索性强
- 低熵:策略集中在少数动作上(如 softmax 尖峰)→ 确定性强,但可能过拟合
对 LLM 而言,每一步 token 的熵 可平均得到 序列级策略熵。
2. Entropy Collapse(熵崩溃)的含义
Entropy collapse 指在 PPO/GRPO 训练过程中,策略熵迅速下降至接近 0,导致模型输出趋于 deterministic(确定性)甚至 degenerate(退化)。
典型表现:
- 模型对所有问题都输出几乎相同的 token 序列(如固定开头、重复模式);
- 生成内容缺乏多样性,即使问题不同;
- 多回答采样(rollout_n)失效:K 个回答几乎完全一样;
- 在数学题中:总用同一种套路,甚至直接输出 “答案:X” 而无推理。
⚠️ 这不是收敛,而是训练崩溃的一种形式——模型“学会作弊”后停止探索。
🤔 二、为什么会出现 Entropy Collapse?(尤其在 LLM + PPO 中)
根本原因:Reward Signal + Policy Update 的正反馈循环
Reward 信号稀疏或有偏
- 例如:只有最终答案正确才有 reward,中间过程无反馈;
- 模型偶然发现一种“高 reward 模板”(如 “解:xxx。答案:3”);
PPO 的 Clipping 机制放大优势
- 一旦某个 action 被赋予高 advantage,PPO 会强烈鼓励它;
- 同时 clipping 阻止了负样本的抑制,导致正样本过拟合;
缺乏探索机制
- LLM 的策略空间极大,但 on-policy 算法只从当前策略采样;
- 一旦策略集中,后续采样无法跳出局部最优;
KL Penalty 若未启用或太弱,无法约束退化
- 若
use_kl_loss=False(如你当前配置),模型可自由坍缩到 deterministic policy。
- 若
💡 Entropy collapse 是“奖励 hack”的自然结果:模型找到 reward 最大化路径后,不再尝试其他可能性。
📊 三、如何观测 Entropy Collapse?
在训练日志中监控:
- 平均策略熵(mean policy entropy):应缓慢下降,但不应趋近 0;
- 回答多样性:对同一 prompt 多次采样,计算 BLEU/Embedding 相似度;
- token 分布:观察 softmax 是否出现“one-hot”倾向。
在 VeRL 中,可以启用
trainer.log_policy_entropy=True(或类似选项)来记录。
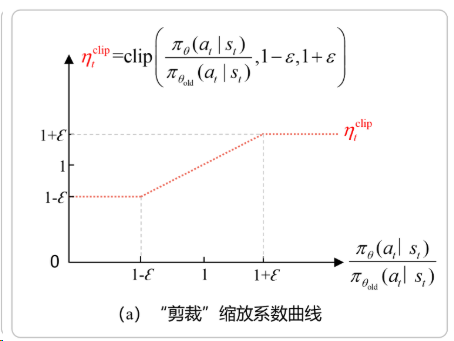
DAPO clip higher
clip 函数有三个参数:
$$
\text{clip}\left( r_{i,t}(\theta),\ 1 - \varepsilon_{\text{low}},\ 1 + \varepsilon_{\text{high}} \right)
$$
这实际上是 PPO 算法中“非对称裁剪(asymmetric clipping)” 的一种变体,相比标准 PPO 的对称裁剪(通常只用一个 (\varepsilon),如 0.2),它允许优势为正和负时使用不同的裁剪边界,从而更精细地控制策略更新。
下面逐个解释这三个参数的含义:
✅ 1. ( r_{i,t}(\theta) ):重要性采样比率(Importance Sampling Ratio)
这是 PPO 的核心:
$$
r_{i,t}(\theta) = \frac{\pi_\theta(a_t | s_t)}{\pi_{\theta_{\text{old}}}(a_t | s_t)}
$$
- 表示当前策略 (\pi_\theta) 与 旧策略 (\pi_{\theta_{\text{old}}}) 在状态 (s_t) 下采取动作 (a_t) 的概率之比;
- 若 (r_{i,t} > 1):当前策略更偏好该动作;
- 若 (r_{i,t} < 1):当前策略更不偏好该动作。
💡 它衡量了“策略更新的幅度”,但直接优化它会导致训练不稳定,因此需要 clip。
✅ 2. (1 - \varepsilon_{\text{low}}):下界裁剪阈值(针对负优势或策略减小)
- (\varepsilon_{\text{low}} > 0)(如 0.2)
- 当 (r_{i,t}(\theta) < 1 - \varepsilon_{\text{low}}) 时,说明当前策略大幅降低了某动作的概率;
- PPO 会将其 裁剪到 (1 - \varepsilon_{\text{low}}),防止策略过快放弃某些动作(保留探索性)。
📌 这主要影响 负优势((\hat{A}_t < 0)) 的样本:即使动作不好,也不允许概率降得太快。
✅ 3. (1 + \varepsilon_{\text{high}}):上界裁剪阈值(针对正优势或策略增大)
- (\varepsilon_{\text{high}} > 0)(如 0.2,也可设为不同值)
- 当 (r_{i,t}(\theta) > 1 + \varepsilon_{\text{high}}) 时,说明当前策略大幅提升了某动作的概率;
- PPO 会将其 裁剪到 (1 + \varepsilon_{\text{high}}),防止策略过激地偏向某些动作(避免崩溃)。
📌 这主要影响 正优势((\hat{A}_t > 0)) 的样本:即使动作好,也不允许概率升得太猛。
📊 标准 PPO vs 非对称 Clip
| 类型 | 裁剪函数 | 特点 |
|---|---|---|
| 标准 PPO | (\text{clip}(r_t, 1-\varepsilon, 1+\varepsilon)) | 对称,(\varepsilon_{\text{low}} = \varepsilon_{\text{high}} = \varepsilon) |
| 非对称 PPO(如 DAPO) | (\text{clip}(r_t, 1-\varepsilon_{\text{low}}, 1+\varepsilon_{\text{high}})) | 可分别控制“增大”和“减小”的步长 |
例如:
- 设 (\varepsilon_{\text{low}} = 0.1),(\varepsilon_{\text{high}} = 0.3)
→ 允许策略更激进地增加好动作的概率,但更保守地减少坏动作的概率(保留探索)。
🧠 为什么需要非对称裁剪?(DAPO 的动机)
在 LLM 强化学习中:
- 正优势样本(正确回答)非常稀疏 → 需要更强的学习信号(允许更大的 (r_t),即更大的 (\varepsilon_{\text{high}}));
- 负优势样本(错误回答)很多 → 但不能一刀切地抛弃,否则 entropy collapse(需更小的 (\varepsilon_{\text{low}}),即裁剪更紧)。
因此,非对称 clip 是对标准 PPO 的改进,尤其适合 reward 稀疏、高维动作空间(如 LLM)的场景。
📌 在 PPO Loss 中如何使用?
完整目标函数为:
$$
L^{\text{PPO}} = \mathbb{E}t \left[ \min\left(
r_t(\theta) \hat{A}t,\
\text{clip}\left(r_t(\theta), 1 - \varepsilon{\text{low}}, 1 + \varepsilon{\text{high}} \right) \hat{A}_t
\right) \right]
$$
- 当 (\hat{A}_t > 0)(好动作):clip 上限防止过拟合;
- 当 (\hat{A}_t < 0)(坏动作):clip 下限防止过放弃。
✅ 总结
| 参数 | 含义 | 典型值 | 作用 |
|---|---|---|---|
| (r_{i,t}(\theta)) | 当前策略 vs 旧策略的概率比 | 动态变化 | 衡量策略变化幅度 |
| (1 - \varepsilon_{\text{low}}) | 概率减小的下限 | 0.8–0.9 | 防止过快放弃动作(保探索) |
| (1 + \varepsilon_{\text{high}}) | 概率增大的上限 | 1.1–1.3 | 防止过激偏向动作(保稳定) |
在 DAPO 等改进算法中,这种非对称设计能缓解 entropy collapse,提升样本利用效率,特别适合你正在做的 多回答、程序化 reward 的 LLM 数学推理训练。
如果你在 VeRL 中看到类似 clip_range_low 和 clip_range_high 的配置项,那就是对应 (\varepsilon_{\text{low}}) 和 (\varepsilon_{\text{high}})。
参考文献
[^11]: DeepSeekMath: Pushing the limits of mathematical reasoning in open language models
[^12]: DAPO: An Open-Source LLM Reinforcement Learning System at Scale
RL Algorithms: PPO & GRPO-like
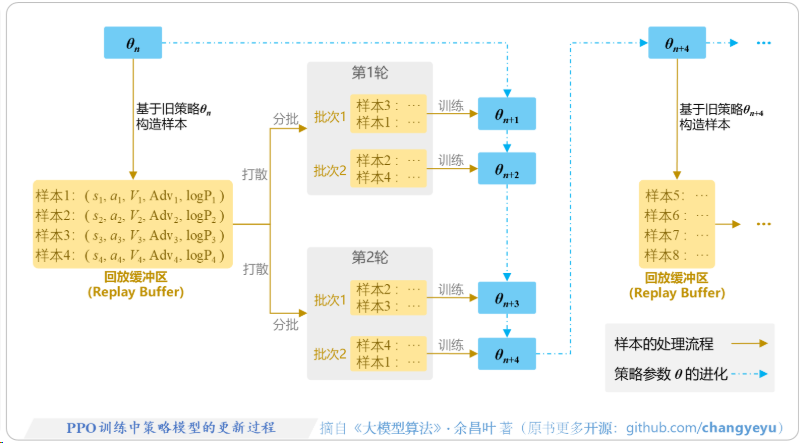 [^13]
[^13]